这个插件可以拦截页面上的 ajax 请求，并把返回结果替换成任意文本。它对 mock 数据、排查一些线上问题等会有很大帮助。（当然 chales 等抓包软件也可以做到，然而使用起来比较繁琐，做成 chrome 插件的形式会方便许多）

以下是使用效果，通过修改 ajax 请求结果，我把第一条文章标题替换成了“这标题特调皮（Σ（ﾟдﾟlll）句内三押×2）”：

使用示例（视频）

http://t.cn/EMvR6pa?m=4347641385182648&u=5352731024

Chrome 商店地址

地址：https://chrome.google.com/webstore/detail/ajax-interceptor/nhpjggchkhnlbgdfcbgpdpkifemomkpg

你也可以直接搜索 Ajax Interceptor 进行安装

注意

1. 当你不需要使用该插件时，建议把开关关上，以免对页面正常浏览造成影响
2. 暂不支持由 fetch 发起的请求

大致原理

页面加载时往页面上注入 js 代码，这段 js 会生成一个 XMLHttpRequest 的代理对象，并把 window.XMLHttpRequest 替换成这个对象。该对象又会对 onreadystatechange 和 onload 两个回调函数做特殊处理，把 responseText 和 response 的值覆盖为你设置的值。更详细的原理推荐看下这篇文章：https://www.jianshu.com/p/7337ac624b8e ，该插件实现原理与之基本类似。
其它就是这段页面上的 js 代码和右侧弹出的 iframe (用户界面)以及插件后台代码一些数据交互和存储上的实现，这部分比较杂就不介绍了~

在平时的代码里，递归是很常见的，然而它可能会带来的调用栈溢出问题有时也令人头疼：

我们知道， js 引擎（包括大部分语言）对于函数调用栈的大小是有限制的，如下图（虽然都是很老的浏览器，但还是有参考价值）：

为了解决递归时调用栈溢出的问题，除了把递归函数改为迭代的形式外，改为尾递归的形式也可以解决（虽然目前大部分浏览器没有对尾递归（尾调用）做优化，依然会导致栈溢出，但了解尾递归的优化方式还是有价值的。而且我们可以通过一个统一的工具函数把尾递归转化为不会溢出的形式，这些下文会一一展开）。
在讨论尾递归之前，我们先了解一下尾调用，以及 js 引擎如何对其进行优化。

尾调用

当函数a的最后一个动作是调用函数b时，那么对函数b的调用形式就是尾调用。比如下面的代码里对fn1的调用就是尾调用：

1
2
3
4
5
6
7
8
9
10
11

const fn1 = (a) => {
  let b = a + 1;
  return b;
}

const fn2 = (x) => {
  let y = x + 1;
  return fn1(y);        // line A
}

const result = fn2(1);  // line B

辨别是否是尾调用

1
2
3

const a = () => {
  b();
}

这里b的调用不是尾调用，因为函数a在调用b后还隐式地执行了一段return undefined，如下面这段代码：

1
2
3
4

const a = () => {
  b();
  return undefined;
}

1
2

const a = () => b() || c();
const a1 = () => b() && c();

这里a和a1中的b都不是尾调用，因为在它调用之后还有判断的动作以及可能的对于c的调用，而c都是尾调用。

1
2
3
4

const a = () => {
  let result = b();
  return result;
}

对于这段代码，有文章指出b并不是尾调用，即便它与const a = () => b()是等价的，而后者显然是尾调用。这就涉及到定义的问题了，我觉得不必过于纠结，尾调用的真正目的是为了进行优化，防止栈溢出，我测试了下支持尾调用的 safari 浏览器，在严格模式下用类似的代码执行一段递归函数，结果是不会导致栈溢出，所以 safari 对这种形式的代码做了优化。

尾递归

现在就轮到本篇文章的主角——尾递归了，看一下下面这段简单的递归代码：

1
2
3
4

const sum = (n) => {
  if (n <= 1) return n;
  return n + sum(n-1)
}

1
2
3
4

const sum = (n, prevSum = 0) => {
  if (n <= 1) return n + prevSum;
  return sum(n-1, n + prevSum)
}

Trampoline

Trampoline是对尾递归函数进行处理的一种技巧。我们需要先把上面的sum函数改造一下，再由trampoline函数处理即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

const sum0 = (n, prevSum = 0) => {
  if (n <= 1) return n + prevSum;
  return () => sum0(n-1, n + prevSum)
}
const trampoline = f => (...args) => {
  let result = f(...args);
  while (typeof result === 'function') {
    result = result();
  }
  return result;
}
const sum = trampoline(sum0);

console.log(sum(1000000)); // 不会栈溢出

当然，如果一个方法可以写成尾递归的形式，那它肯定也能被写成迭代的形式，但有些场景下使用递归可能会更加直观，如果它能被转为尾递归，你就可以直接用trampoline函数进行处理，或者把它改写成迭代的方法（或者等大部分浏览器支持尾递归优化后在严格模式下执行）

参考：

https://blog.logrocket.com/using-trampolines-to-manage-large-recursive-loops-in-javascript-d8c9db095ae3
http://2ality.com/2015/06/tail-call-optimization.html
https://www.zhihu.com/question/30078697/answer/146047599

上一篇我们研究了 Immutable.js 持久化数据结构的基本实现原理，对其核心数据结构Vector Trie进行了介绍，并着重探究了其中的位分区机制。采用位分区的根本原因是为了优化速度，而对于空间的优化， Immutable.js 是怎么做的呢？接下来先探讨下这点。

HAMT

HAMT全称hash array mapped trie，其基本原理与上篇所说的Vector Trie非常相似，不过它会对树进行压缩，以节约一些空间。 Immutable.js 参考了HAMT对树进行了高度和节点内部的压缩。

树高压缩

假设我们有一个 2 叉 Vector Trie，现在存了一个值，key为110，它会被存到0 1 1这条路径下，如下图：

显然，这图里展示的结构已经进行了最简单的优化，因为现在只存了一个值，所以把与110无关的节点去掉了。还能进行什么优化吗？我们发现，中间那两个节点也是可以去掉的，如下图：

获取该值时，我们先从0找下来，发现这直接是一个根节点，那取它存储的值就行了。就是说在不产生混淆的情况下，我们可以用尽可能少的二进制位去标识这个 key 。这样我们就进行了高度上的压缩，既减少了空间，又减少了查找和修改的时间。
如果要添加一个值，它的 key 结尾也是0，该怎么做呢？很简单，如下图：

我们只要在需要的时候增加或减少节点即可。

节点内部压缩-Bitmap

上一篇我们提到， Immutable.js 的 Trie 里，每个节点数组的长度是 32 ，然而在很多情况下，这 32 个位置大部分是用不到的，这么大的数组显然也占用了很大空间。使用Bitmap，我们就可以对数组进行压缩。
我们先拿长度为 8 的数组举例：

我们实际上只是用了数组的下标对 key 进行索引，这样想数组第 5、6、7 位显然目前是毫无作用的，那 0、2、3 呢？我们有必要为了一个下标 4 去维持一个长度为5的数组吗？我们只需要指明“假想数组”中下标为 1 和为 4 的位置有数就可以了。这里就可以用到bitmap，如下：

我们采用了一个数，以其二进制形式表达“假想的长度为8的数组”中的占位情况，1 表示数组里相应下标位置有值，0 则表示相应位置为空。比如这个二进制数第 4 位（从右往左，从 0 开始数）现在是 1 ，就表示数组下标为 4 的位置有值。这样原本的长度为 8 的数组就可以压缩到 2 。
注意这个数组中的元素还是按照“假想数组”中的顺序排列的，这样我们若要取“假想数组”中下标为 i 的元素时，首先是判断该位置有没有值，若有，下一步就是得到在它之前有几个元素，即在二进制数里第 i 位之前有多少位为 1 ，假设数量为 a ，那么该元素在当前压缩后的数组里下标就是 a 。
具体操作中，我们可以通过bitmap & (1 << i - 1)，得到一个二进制数，该二进制数中只有第 i 位之前有值的地方为 1 ，其余全为 0 ，下面我们只需统计该二进制数里 1 的数量即可得到下标。计算二进制数中 1 数量的过程被称作popcount，具体算法有很多，我了解不多就不展开了，前面点击后是维基的地址，感兴趣的可以研究下。
下面我们看一下这部分的源码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

get(shift, keyHash, key, notSetValue) {
  if (keyHash === undefined) {
    keyHash = hash(key);
  }
  const bit = 1 << ((shift === 0 ? keyHash : keyHash >>> shift) & MASK);
  const bitmap = this.bitmap;
  return (bitmap & bit) === 0
    ? notSetValue
    : this.nodes[popCount(bitmap & (bit - 1))].get(
        shift + SHIFT,
        keyHash,
        key,
        notSetValue
      );
}

1
2
3
4
5
6
7
8

function popCount(x) {
  x -= (x >> 1) & 0x55555555;
  x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
  x = (x + (x >> 4)) & 0x0f0f0f0f;
  x += x >> 8;
  x += x >> 16;
  return x & 0x7f;
}

为什么是32

上一篇我们提到了 Immutable.js 的 Vector Trie 采用了 32 作为数组的长度，也解释了由于采用了位分区，该数字只能是2的整数次幂，所以不能是 31、33 等。但8、16、64等等呢？这是通过实际测试得出的，见下图：

图中分别是查找和更新的时间，看上去似乎 8 或 16 更好？考虑到平时的使用中，查找比更新频次高很多，所以 Immutable.js 选择了 32。

回顾

现在，我们就能理解第一篇文章开头的截图了：


我们可以看到， map 里主要有三种类型的节点：

• HashArrayMapNode，拥有的子节点数量 ＞16 ，拥有的数组长度为 32
• BitmapIndexedNode，拥有的子节点数量 ≤16 ，拥有的数组长度与子节点数量一致，经由 bitmap 压缩
• ValueNode，叶子节点，存储 key 和 value

此外，每个节点似乎都有个ownerID属性，这又是做什么的呢？它涉及到 Immutable.js 中的可变数据结构。

Transient

其实可以说 Immutable.js 中的数据结构有两种形态，“不可变”和“可变”。虽然“不可变”是 Immutable.js 的主要优势，但“可变”形态下的操作当然效率更高。有时对于某一系列操作，我们只需要得到这组操作结束后的状态，若中间的每一个操作都用不可变数据结构去实现显然有些多余。这种情景下，我们就可以使用withMutations方法对相应数据结构进行临时的“可变”操作，最后再返回一个不可变的结构，这就是Transient，比如这样：

1
2
3
4
5
6
7
8

let map = new Immutable.Map({});
map = map.withMutations((m) => {
  // 开启Transient
  m.set('a', 1); // 我们可以直接在m上进行修改，不需要 m = m.set('a', 1)
  m.set('b', 2);
  m.set('c', 3);
});
// Transient结束

1. 若要操作的节点的ownerID与父节点的不一致，则生成新的节点，把旧节点上的值拷贝过来，其ownerID更新为父节点的ownerID，然后进行相应操作；
2. 若要操作的节点的ownerID与父节点的一致，则直接在该节点上操作；
   下面先我们看下 Immutable.js 中开启Transient的相关源码：

   1	function OwnerID() {}

   1 2 3

   function asMutable() { return this.__ownerID ? this : this.__ensureOwner(new OwnerID()); }

   1 2 3 4 5

   function withMutations(fn) { const mutable = this.asMutable(); fn(mutable); return mutable.wasAltered() ? mutable.__ensureOwner(this.__ownerID) : this; }

   它给了根节点一个ownerID，这个ownerID会在接下来的操作中按照上面的逻辑使用。这段代码有个“骚操作”，就是用 JS 的对象地址去作为 ID ，因为每次 new 之后的对象的地址肯定与之前的对象不同，所以用这种方法可以很简便高效地构造一套 ID 体系。
   下面再看下开启后进行操作时的一段源码（ Map 中的set操作就会调用这个update方法）：

   1 2 3 4 5 6 7 8 9 10 11 12 13

   update(ownerID, shift, keyHash, key, value, didChangeSize, didAlter) { // ...省略前面的代码 const isEditable = ownerID && ownerID === this.ownerID; const newNodes = setAt(nodes, idx, newNode, isEditable); if (isEditable) { this.count = newCount; this.nodes = newNodes; return this; } return new HashArrayMapNode(ownerID, newCount, newNodes); }

   与前面讲的逻辑一样，先比较该节点ownerID与传进来父节点的是否一致，然后直接在节点上操作或生成新的节点。

hash冲突

这块的内容就没什么新东西了，任何语言或库里对于 hashMap 的实现都需考虑到 hash 冲突的问题。我们主要看一下 Immutable.js 是怎么处理的。
要上一篇我们知道了，在往 Map 里存一对 key、value 时， Immutable.js 会先对 key 进行 hash ，根据 hash 后的值存到树的相应位置里。不同的 key 被 hash 后的结果是可能相同的，即便概率应当很小。
hash 冲突是一个很基本的问题，解决方法有很多，这里最简单适用的方法就是把冲突的节点扩展成一个线性结构，即数组，数组里直接存一组组 key 和 value ，查找到此处时则遍历该数组找到匹配的 key 。虽然这里的时间复杂度会变成线性的，但考虑到发生 hash 冲突的概率很低，所以时间复杂度的增加可以忽略不计。
我发现 Immutable.js 的 hash 函数对abc和bCc的 hash 结果都是 96354，在同一个 map 里用这两个 key 就会造成 hash 冲突，我们把这个 map log 出来如下：

Immutable.js 用了一个叫做HashCollisionNode的节点去处理发生冲突的键值，它们被放在entries数组里。
大家也可以自己试试，代码如下：

1
2
3
4
5
6
7
8
9
10

let map = new Immutable.Map({});

for (let i = 0; i < 10; i++) {
  map = map.set(Math.random(), i); // 随便塞一点别的数据
}

map = map.set('abc', 'value1');
map = map.set('bCc', 'value2');

console.log(map)

参考：

https://hypirion.com/musings/understanding-persistent-vector-pt-1
https://io-meter.com/2016/11/06/functional-go-intro-to-hamt
https://cdn.oreillystatic.com/en/assets/1/event/259/Immutable%20data%20structures%20for%20functional%20JavaScript%20Presentation.pdf
https://infoscience.epfl.ch/record/169879/files/RMTrees.pdf
http://lampwww.epfl.ch/papers/idealhashtrees.pdf
https://github.com/funfish/blog
https://github.com/facebook/immutable-js/blob/e65e5af806ea23a32ccf8f56c6fabf39605bac80/src

Immutable.js 由 Facebook 花费 3 年时间打造，为前端开发提供了很多便利，如今 React+Redux+Immutable.js 的组合已经成为许多项目的标配。我们知道 Immutable.js 采用了持久化数据结构和结构共享，保证每一个对象都是不可变的，任何添加、修改、删除等操作都会生成一个新的对象，且通过结构共享等方式大幅提高性能。
网上已经有很多文章简单介绍了 Immutable.js 的原理，但基本都是浅尝辄止，我也是搜了很久没找到针对 Immutable.js 原理的相对深入详细的文章，中英文都没有，针对 Clojure 或 Go 中持久化数据结构实现的文章倒是有一些。本文会集合多方资料以及我自己的一些理解，深入一些探究 Immutable.js 实现机制。
由于需要探讨的内容较长，写起来也比较费时，所以该系列会分成二到三篇文章完成。

Immutable.js 部分参考了 Clojure 中的PersistentVector的实现方式，并有所优化和取舍，本文的一些内容也是基于它，想了解的可以阅读这里（共五篇，这是第一篇）

简单的例子

在深入研究前，我们先看个简单的例子：

1
2
3
4
5
6
7

let map1 = Immutable.Map({});

for (let i = 0; i < 800; i++) {
  map1 = map1.set(Math.random(), Math.random());
}

console.log(map1);

大致看个形状就行了，下面我们会由浅入深逐步揭开它的面纱。

基本原理

我们先看下维基对于持久化数据结构的定义：

In computing, a persistent data structure is a data structure that always preserves the previous version of itself when it is modified.

通俗点解释就是，对于一个持久化数据结构，每次修改后我们都会得到一个新的版本，且旧版本可以完好保留。

Immutable.js 用树实现了持久化数据结构，先看下图这颗树：

假如我们要在g下面插入一个节点h，如何在插入后让原有的树保持不变？最简单的方法当然是重新生成一颗树：

但这样做显然是很低效的，每次操作都需要生成一颗全新的树，既费时又费空间，因而有了如下的优化方案：

我们新生成一个根节点，对于有修改的部分，把相应路径上的所有节点重新生成，对于本次操作没有修改的部分，我们可以直接把相应的旧的节点拷贝过去，这其实就是结构共享。这样每次操作同样会获得一个全新的版本（根节点变了，新的a!==旧的a），历史版本可以完好保留，同时也节约了空间和时间。
至此我们发现，用树实现持久化数据结构还是比较简单的，Immutable.js提供了多种数据结构，比如回到开头的例子，一个map如何成为持久化数据结构呢？

Vector Trie

实际上对于一个map，我们完全可以把它视为一颗扁平的树，与上文实现持久化数据结构的方式一样，每次操作后生成一个新的对象，把旧的值全都依次拷贝过去，对需要修改或添加的属性，则重新生成。这其实就是Object.assign，然而这样显然效率很低，有没有更好的方法呢？
在实现持久化数据结构时，Immutable.js 参考了Vector Trie这种数据结构（其实更准确的叫法是persistent bit-partitioned vector trie或bitmapped vector trie，这是Clojure里使用的一种数据结构，Immutable.js 里的相关实现与其很相似），我们先了解下它的基本结构。
假如我们有一个 map ，key 全都是数字（当然你也可以把它理解为数组）{0: ‘banana’, 1: ‘grape’, 2: ‘lemon’, 3: ‘orange’, 4: ‘apple’}，为了构造一棵二叉Vector Trie，我们可以先把所有的key转换为二进制的形式：{‘000’: ‘banana’, ‘001’: ‘grape’, ‘010’: ‘lemon’, ‘011’: ‘orange’, ‘100’: ‘apple’}，然后如下图构建Vector Trie：

可以看到，Vector Trie的每个节点是一个数组，数组里有0和1两个数，表示一个二进制数，所有值都存在叶子节点上，比如我们要找001的值时，只需顺着0 0 1找下来，即可得到grape。那么想实现持久化数据结构当然也不难了，比如我们想添加一个5: ‘watermelon’：

可见对于一个 key 全是数字的map，我们完全可以通过一颗Vector Trie来实现它，同时实现持久化数据结构。如果key不是数字怎么办呢？转成数字就行了。 Immutable.js 实现了一个hash函数，可以把一个值转换成相应数字。
这里为了简化，每个节点数组长度仅为2，这样在数据量大的时候，树会变得很深，查询会很耗时，所以可以扩大数组的长度，Immutable.js 选择了32。为什么不是31？40？其实数组长度必须是2的整数次幂，这里涉及到实现Vector Trie时的一个优化，接下来我们先研究下这点。

数字分区（Digit partitioning）

数字分区指我们把一个 key 作为数字对应到一棵前缀树上，正如上节所讲的那样。
假如我们有一个 key 9128，以 7 为基数，即数组长度是 7，它在Vector Trie里是这么表示的：

需要5层数组，我们先找到3这个分支，再找到5，之后依次到0。为了依次得到这几个数字，我们可以预先把9128转为7进制的35420，但其实没有这个必要，因为转为 7 进制形式的过程就是不断进行除法并取余得到每一位上的数，我们无须预先转换好，类似的操作可以在每一层上依次执行。
运用进制转换相关的知识，我们可以采用这个方法key / radixlevel - 1 % radix得到每一位的数（为了简便，本文除代码外所有/符号皆表示除法且向下取整），其中radix是每层数组的长度，即转换成几进制，level是当前在第几层，即第几位数。比如这里key是9128，radix是7，一开始level是5，通过这个式子我们可以得到第一层的数3。
代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12

const RADIX = 7;

function find(key) {
  let node = root; // root是根节点，在别的地方定义了

  // depth是当前树的深度。这种计算方式跟上面列出的式子是等价的，但可以避免多次指数计算
  for (let size = Math.pow(RADIX, (depth - 1)); size > 1; size /= RADIX) {
    node = node[Math.floor(key / size) % RADIX];
  }

  return node[key % RADIX];
}

位分区（Bit Partitioning）

显然，以上数字分区的方法是有点耗时的，在每一层我们都要进行两次除法一次取模，显然这样并不高效，位分区就是对其的一种优化。
位分区实际上是数字分区的一个子集，所有以2的整数次幂（2，4，8，16，32…）为基数的数字分区前缀树，都可以转为位分区。基于一些位运算相关的知识，我们就能避免一些耗时的计算。
数字分区把 key 拆分成一个个数字，而位分区把 key 分成一组组 bit。比如一个 32 路的前缀树，数字分区的方法是把 key 以 32 为基数拆分（实际上就是32进制），而位分区是把它以 5bit 拆分，实际上就是把 32 进制数的每一位看做 5 个 bit ，或者说把 32 进制数看做2进制进行操作，这样原本的很多计算就可以用更高效的位运算的方式代替。因为现在基数是 32，即radix为 32，所以前面的式子现在是key / 32level - 1 % 32，而 32 又可以写作25，那么该式子可以转成这样key / 25 × (level - 1) % 25。根据位运算相关的知识我们知道a / 2n === a >>> n 、a % 2n === a & (n - 1) 。
如果你对位运算不太熟悉的话，大可不看上面的式子，举个例子就好理解了：比如数字666666的二进制形式是10100 01011 00001 01010，这是一个20位的二进制数。如果我们要得到第二层那五位数01011，我们可以先把它右移>>>(左侧补0)10位，得到00000 00000 10100 01011，再&一下00000 00000 00000 11111，就得到了01011。
这样我们可以得到下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13

const SHIFT = 5;
const WIDTH = 1 << SHIFT, //  32
const MASK = WIDTH - 1; // 31，即11111

function find(key) {
  let node = root; 

  for (let shift = (depth - 1) * SHIFT; shift > 0; shift -= SHIFT) {
    node = node[(key >>> shift) & MASK];
  }

  return node[key & MASK];
}

源码

说了这么多，我们看一下 Immutable.js 的源码吧。我们主要看一下查找的部分就够了，这是Vector Trie的核心。

1
2
3
4
5
6
7
8
9
10

get(shift, keyHash, key, notSetValue) {
  if (keyHash === undefined) {
    keyHash = hash(key);
  }
  const idx = (shift === 0 ? keyHash : keyHash >>> shift) & MASK;
  const node = this.nodes[idx];
  return node
    ? node.get(shift + SHIFT, keyHash, key, notSetValue)
    : notSetValue;
}

时间复杂度

因为采用了结构共享，在添加、修改、删除操作后，我们避免了将 map 中所有值拷贝一遍，所以特别是在数据量较大时，这些操作相比Object.assign有明显提升。
然而，查询速度似乎减慢了？我们知道 map 里根据 key 查找的速度是O(1)，这里由于变成了一棵树，查询的时间复杂度变成了O(log N)，准确说是O(log32 N)。
等等 32 叉树？这棵树可不是一般地宽啊，Javascript里对象可以拥有的key的最大数量一般不会超过232个（ECMA-262第五版里定义了JS里由于数组的长度本身是一个 32 位数，所以数组长度不应大于 2³² - 1 ，JS里对象的实现相对复杂，但大部分功能是建立在数组上的，所以在大部分场景下对象里 key 的数量不会超过 2³² - 1。相关讨论见这里），这样就可以把查找的时间复杂度当做是“O(log32 232)”，差不多就是“O(log 7)”，所以我们可以认为在实际运用中，5bit (32路)的 Vector Trie 查询的时间复杂度是常数级的，32 叉树就是用了空间换时间。
空间…这个 32 叉树占用的空间也太大了吧？即便只有三层，我们也会有超过32 × 32 × 32 = 32768个节点。当然 Immutable.js 在具体实现时肯定不会傻乎乎的占用这么大空间，它对树的高度和宽度都做了“压缩”，此外，还对操作效率进行了其它一些优化，比如对 list 进行了“tail优化”。相关内容我们下一章讨论。

参考：

https://hypirion.com/musings/understanding-persistent-vector-pt-1
https://io-meter.com/2016/09/03/Functional-Go-persist-datastructure-intro
https://cdn.oreillystatic.com/en/assets/1/event/259/Immutable%20data%20structures%20for%20functional%20JavaScript%20Presentation.pdf
https://michael.steindorfer.name/publications/oopsla15.pdf
https://github.com/facebook/immutable-js/blob/e65e5af806ea23a32ccf8f56c6fabf39605bac80/src

HTTPS的加密机制（SSL/TLS）虽然是个前端后端ios安卓等都应了解的基本问题，但不少人对它的了解都浮于表面，有很多关键机制没有彻底弄明白。网上的很多HTTPS相关文章也总会忽略一些内容，我学习它的时候也废了挺大功夫。
对称加密、非对称加密、数字签名、数字证书等等，在学习过程中，除了了解“它是什么”，你是否有想过“为什么是它”、“为什么不是xxx”？我认为理解了后两个问题才真正理解了HTTPS的加密机制。
本文以问题的形式逐步展开，一步步解开HTTPS的面纱，希望能帮助你彻底搞懂HTTPS。特别是对于了解过HTTPS却在有些地方有所卡壳的人，希望本文能帮助你理清思路。

为什么需要加密？

因为http的内容是明文传输的，明文数据会经过中间代理服务器、路由器、wifi热点、通信服务运营商等多个物理节点，如果信息在传输过程中被劫持，传输的内容就完全暴露了，他还可以篡改传输的信息且不被双方察觉，这就是中间人攻击。所以我们才需要对信息进行加密。

什么是对称加密？

就是有一个密钥，它可以对一段内容加密，加密后只能用它才能解密看到原本的内容，就和我们日常生活中用的钥匙作用一样。

用对称加密可行吗？

如果通信双方都各自持有同一个密钥，且没有别人知道，这两方的通信安全当然是可以被保证的（除非密钥被破解）。
然而最大的问题就是这个密钥怎么让传输的双方知晓，同时不被别人知道。如果由服务器生成一个密钥并传输给浏览器，那这个传输过程中密钥被别人劫持弄到手了怎么办？之后他就能用密钥解开双方传输的任何内容了，所以这么做当然不行。
换种思路？试想一下，如果浏览器内部就预存了网站A的密钥，且可以确保除了浏览器和网站A，不会有任何外人知道该密钥，那理论上用对称加密是可以的，这样浏览器只要预存好世界上所有HTTPS网站的密钥就行啦！这么做显然不现实。（那在自己的ios或安卓的app里预先藏入自己服务器的密钥，通过对称加密的方式与服务器通信可以吗？我认为一般是可以的，但是一定要对密钥做好防护）
怎么办？所以我们就需要神奇的非对称加密

什么是非对称加密？

有两把密钥，通常一把叫做公钥、一把叫做私钥，用公钥加密的内容必须用私钥才能解开，同样，私钥加密的内容只有公钥能解开。

用非对称加密可行吗？

鉴于非对称加密的机制，我们可能会有这种思路：服务器先把公钥直接明文传输给浏览器，之后浏览器向服务器传数据前都先用这个公钥加密好再传，这条数据的安全似乎可以保障了！因为只有服务器有相应的私钥能解开这条数据。
然而由服务器到浏览器的这条路怎么保障安全？如果服务器用它的的私钥加密数据传给浏览器，那么浏览器用公钥可以解密它，而这个公钥是一开始通过明文传输给浏览器的，这个公钥被谁劫持到的话，他也能用该公钥解密服务器传来的信息了。所以目前似乎只能保证由浏览器向服务器传输数据时的安全性（其实仍有漏洞，下文会说），那利用这点你能想到什么解决方案吗？

改良的非对称加密方案，似乎可以？

我们已经理解通过一组公钥私钥，已经可以保证单个方向传输的安全性，那用两组公钥私钥，是不是就能保证双向传输都安全了？请看下面的过程：

1. 某网站拥有用于非对称加密的公钥A、私钥A’；浏览器拥有用于非对称加密的公钥B、私钥B’。
2. 浏览器像网站服务器请求，服务器把公钥A明文给传输浏览器。
3. 浏览器把公钥B明文传输给服务器。
4. 之后浏览器向服务器传输的所有东西都用公钥A加密，服务器收到后用私钥A’解密。由于只有服务器拥有这个私钥A’可以解密，所以能保证这条数据的安全。
5. 服务器向浏览器传输的所有东西都用公钥B加密，浏览器收到后用私钥B’解密。同上也可以保证这条数据的安全。

的确可以！抛开这里面仍有的漏洞不谈（下文会讲），HTTPS的加密却没使用这种方案，为什么？最主要的原因是非对称加密算法非常耗时，特别是加密解密一些较大数据的时候有些力不从心，而对称加密快很多，看来必须得用对称加密，那我们能不能运用非对称加密的特性解决前面提到的对称加密的问题？

非对称加密+对称加密？

既然非对称加密耗时，非对称加密+对称加密结合可以吗？而且得尽量减少非对称加密的次数。当然是可以的，而且非对称加密、解密各只需用一次即可。
请看一下这个过程：

1. 某网站拥有用于非对称加密的公钥A、私钥A’。
2. 浏览器像网站服务器请求，服务器把公钥A明文给传输浏览器。
3. 浏览器随机生成一个用于对称加密的密钥X，用公钥A加密后传给服务器。
4. 服务器拿到后用私钥A’解密得到密钥X。
5. 这样双方就都拥有密钥X了，且别人无法知道它。之后双方所有数据都用密钥X加密解密。

完美！HTTPS基本就是采用了这种方案。完美？还是有漏洞的。

中间人攻击

中间人的确无法得到浏览器生成的密钥B，这个密钥本身被公钥A加密了，只有服务器才有私钥A’解开拿到它呀！然而中间人却完全不需要拿到密钥A’就能干坏事了。请看：

1. 某网站拥有用于非对称加密的公钥A、私钥A’。
2. 浏览器向网站服务器请求，服务器把公钥A明文给传输浏览器。
3. 中间人劫持到公钥A，保存下来，把数据包中的公钥A替换成自己伪造的公钥B（它当然也拥有公钥B对应的私钥B’）。
4. 浏览器随机生成一个用于对称加密的密钥X，用公钥B（浏览器不知道公钥被替换了）加密后传给服务器。
5. 中间人劫持后用私钥B’解密得到密钥X，再用公钥A加密后传给服务器。
6. 服务器拿到后用私钥A’解密得到密钥X。

这样在双方都不会发现异常的情况下，中间人得到了密钥B。根本原因是浏览器无法确认自己收到的公钥是不是网站自己的。那么下一步就是解决下面这个问题：

如何证明浏览器收到的公钥一定是该网站的公钥？

现实生活中，如果想证明某身份证号一定是小明的，怎么办？看身份证。这里政府机构起到了“公信”的作用，身份证是由它颁发的，它本身的权威可以对一个人的身份信息作出证明。互联网中能不能搞这么个公信机构呢？给网站颁发一个“身份证”？

数字证书

网站在使用HTTPS前，需要向“CA机构”申请颁发一份数字证书，数字证书里有证书持有者、证书持有者的公钥等信息，服务器把证书传输给浏览器，浏览器从证书里取公钥就行了，证书就如身份证一样，可以证明“该公钥对应该网站”。然而这里又有一个显而易见的问题了，证书本身的传输过程中，如何防止被篡改？即如何证明证书本身的真实性？身份证有一些防伪技术，数字证书怎么防伪呢？解决这个问题我们就基本接近胜利了！

如何放防止数字证书被篡改？

我们把证书内容生成一份“签名”，比对证书内容和签名是否一致就能察觉是否被篡改。这种技术就叫数字签名：

数字签名

这部分内容建议看下图并结合后面的文字理解，图中左侧是数字签名的制作过程，右侧是验证过程（原图出处找不到了，可以看出来这图已经被转载了无数次了。。。）

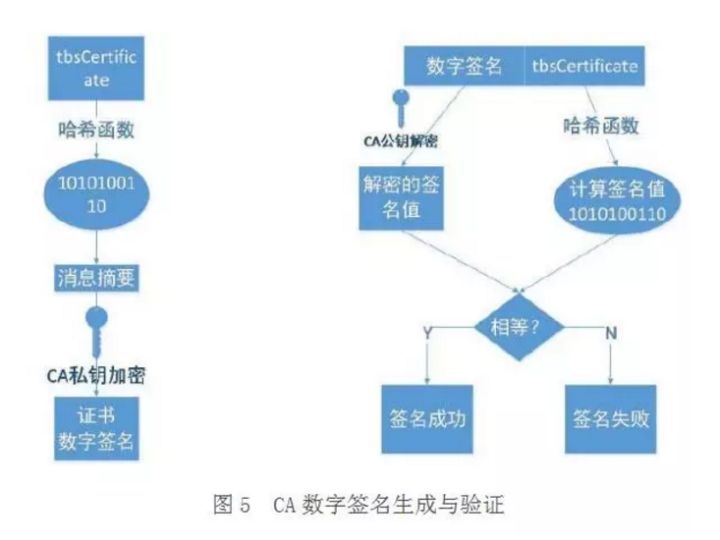
数字签名的制作过程：

1. CA拥有非对称加密的私钥和公钥。
2. CA对证书明文信息进行hash。
3. 对hash后的值用私钥加密，得到数字签名。

明文和数字签名共同组成了数字证书，这样一份数字证书就可以颁发给网站了。
那浏览器拿到服务器传来的数字证书后，如何验证它是不是真的？（有没有被篡改、掉包）

浏览器验证过程：

1. 拿到证书，得到明文T，数字签名S。
2. 用CA机构的公钥对S解密（由于是浏览器信任的机构，所以浏览器保有它的公钥。详情见下文），得到S’。
3. 用证书里说明的hash算法对明文T进行hash得到T’。
4. 比较S’是否等于T’，等于则表明证书可信。

为什么这样可以证明证书可信呢？我们来仔细想一下。

中间人有可能篡改该证书吗？

假设中间人篡改了证书的原文，由于他没有CA机构的私钥，所以无法得到此时加密后签名，无法相应地篡改签名。浏览器收到该证书后会发现原文和签名解密后的值不一致，则说明证书已被篡改，证书不可信，从而终止向服务器传输信息，防止信息泄露给中间人。
既然不可能篡改，那整个证书被掉包呢？

中间人有可能把证书掉包吗？

假设有另一个网站B也拿到了CA机构认证的证书，它想搞垮网站A，想劫持网站A的信息。于是它成为中间人拦截到了A传给浏览器的证书，然后替换成自己的证书，传给浏览器，之后浏览器就会错误地拿到B的证书里的公钥了，会导致上文提到的漏洞。
其实这并不会发生，因为证书里包含了网站A的信息，包括域名，浏览器把证书里的域名与自己请求的域名比对一下就知道有没有被掉包了。

为什么制作数字签名时需要hash一次？

我初学HTTPS的时候就有这个问题，似乎以上过程中hash有点多余，把hash过程去掉也能保证证书没有被篡改。
最显然的是性能问题，前面我们已经说了非对称加密效率较差，证书信息一般较长，比较耗时。而hash后得到的是固定长度的信息（比如用md5算法hash后可以得到固定的128位的值），这样加密解密就会快很多。
当然还有安全上的原因，这部分内容相对深一些，感兴趣的可以看这篇解答：https://crypto.stackexchange.com/a/12780

怎么证明CA机构的公钥是可信的？

你们可能会发现上文中说到CA机构的公钥，我几乎一笔带过，“浏览器保有它的公钥”，这是个什么保有法？怎么证明这个公钥是否可信？
让我们回想一下数字证书到底是干啥的？没错，为了证明某公钥是可信的，即“该公钥是否对应该网站/机构等”，那这个CA机构的公钥是不是也可以用数字证书来证明？没错，操作系统、浏览器本身会预装一些它们信任的根证书，如果其中有该CA机构的根证书，那就可以拿到它对应的可信公钥了。

实际上证书之间的认证也可以不止一层，可以A信任B，B信任C，以此类推，我们把它叫做信任链或数字证书链，也就是一连串的数字证书，由根证书为起点，透过层层信任，使终端实体证书的持有者可以获得转授的信任，以证明身份。

另外，不知你们是否遇到过网站访问不了、提示要安装证书的情况？这里安装的就是跟证书。说明浏览器不认给这个网站颁发证书的机构，那么没有该机构的根证书，你就得手动下载安装（风险自己承担XD）。安装该机构的根证书后，你就有了它的公钥，就可以用它验证服务器发来的证书是否可信了。

HTTPS必须在每次请求中都要先在SSL/TLS层进行握手传输密钥吗？

这也是我当时的困惑之一，显然每次请求都经历一次密钥传输过程非常耗时，那怎么达到只传输一次呢？用session就行。
服务器会为每个浏览器（或客户端软件）维护一个session ID，在TSL握手阶段传给浏览器，浏览器生成好密钥传给服务器后，服务器会把该密钥存到相应的session ID下，之后浏览器每次请求都会携带session ID，服务器会根据session ID找到相应的密钥并进行解密加密操作，这样就不必要每次重新制作、传输密钥了！

总结

至此，我们已自下而上地打通了HTTPS加密的整个脉络以及核心知识点，不知你是否真正搞懂了HTTPS呢？
找几个时间，多看、多想、多理解几次就会越来越清晰的！

那么，下面的问题你是否已经可以解答了呢？

1. 为什么要用对称加密+非对称加密？
2. 为什么不能只用非对称加密？
3. 为什么需要数字证书？
4. 为什么需要数字签名？
   …

这篇文章也是对我学习时的一些总结和我自己的理解，希望也能给你一些收获~

white-space、word-break、word-wrap（overflow-wrap）估计是css里最基本又最让人迷惑的三个属性了，我也是经常搞混，所以今天我们就把这三个属性彻底搞清楚。

测试代码

(文末有本文中所有例子的代码)
下面是本文中用于测试各个样式展现情况的html代码：

1
2
3
4
5
6
7

<div id="box">
  Hi&nbsp;&nbsp;,
  This   is a incomprehensibilities long word.
  </br>
  你好&nbsp;&nbsp;，
  这   是一个不可思议的长单词
</div>

white-space

正如它的名字，这个属性是用来控制空白字符的显示的，同时还能控制是否自动换行。它有五个值：normal | nowrap | pre | pre-wrap | pre-line。因为默认是normal，所以我们主要研究下其它四种值时的展现情况。

（为了方便比较，下文所有图，左侧为normal即初始情况，右侧为赋上相应值时的情况）

先看下white-space:nowrap时的情况：

不仅空格被合并，换行符无效，连原本的自动换行都没了！只有</br>才能导致换行！所以这个值的表现还是挺简单的，我们可以理解为永不换行。

white-space:pre：

空格和换行符全都被保留了下来！不过自动换行还是没了。保留，所以pre其实是preserve的缩写，这样就好记了。

white-space:pre-wrap：

显然pre-wrap就是preserve+wrap，保留空格和换行符，且可以自动换行。

white-space:pre-line：

空格被合并了，但是换行符可以发挥作用，line应该是new line的意思，自动换行还在，所以pre-line其实是preserve+new line+wrap。

我整理了一个表予以总结：

word-break

从这个名字可以知道，这个属性是控制单词如何被拆分换行的。它有三个值：normal | break-all | keep-all。

word-break:keep-all：

所有“单词”一律不拆分换行，注意，我这里的“单词”包括连续的中文字符（还有日文、韩文等），或者可以理解为只有空格可以触发自动换行

word-break:break-all：

所有单词碰到边界一律拆分换行，不管你是incomprehensibilities这样一行都显示不下的单词，还是long这样很短的单词，只要碰到边界，都会被强制拆分换行。所以用word-break:break-all时要慎重呀。
这样的效果好像并不太好呀，能不能就把incomprehensibilities拆一下，其它的单词不拆呢？那就需要下面这个属性了：

word-wrap（overflow-wrap）

word-wrap又叫做overflow-wrap：

word-wrap 属性原本属于微软的一个私有属性，在 CSS3 现在的文本规范草案中已经被重名为 overflow-wrap 。 word-wrap 现在被当作 overflow-wrap 的 “别名”。 稳定的谷歌 Chrome 和 Opera 浏览器版本支持这种新语法。

这个属性也是控制单词如何被拆分换行的，实际上是作为word-break的互补，它只有两个值：normal | break-word，那我们看下break-word：

终于达到了上文我们希望的效果，只有当一个单词一整行都显示不下时，才会拆分换行该单词。
所以我觉得overflow-wrap更好理解好记一些，overflow，只有长到溢出的单词才会被强制换行！

（其实前面的word-break属性除了列出的那三个值外，也有个break-word值，效果跟这里的word-wrap:break-word一样，然而只有Chrome、Safari等部分浏览器支持）

总结

最后总结一下三个属性

• white-space，控制空白字符的显示，同时还能控制是否自动换行。它有五个值：normal | nowrap | pre | pre-wrap | pre-line
• word-break，控制单词如何被拆分换行。它有三个值：normal | break-all | keep-all
• word-wrap（overflow-wrap）控制长度超过一行的单词是否被拆分换行，是word-break的补充，它只有两个值：normal | break-word

相信读完了本文，你应该对white-space、word-break、word-wrap有比较系统的认识了吧，如果短时间还是记不住，常看一看就能记住的~

下面是本文里所有例子的代码的地址，每个属性做成了选项，方便操作学习~

我们都知道JavaScript本身并没有共有、私有属性的概念，不过我们可以通过一些方式实现私有属性。
WeakMap也是ES6里就有了，不过我曾一直不太了解它的应用场景，看到有文章说用它的应用场景之一是实现私有属性。怎么实现？为何要用它实现？
关于用WeakMap实现私有属性的方式，本文会从它最原始的面貌看起，理解使用WeakMap的意义。

闭包-可行吗？

提到“私有”的实现方式，我的第一反应就是闭包，似乎可行：

1
2
3
4
5
6
7
8
9
10
11
12
13

const Person = (function() {
  let name;

  function Person(n) {
      name = n;
  }

  Person.prototype.getName = function() {
      return name;
  };

  return Person;
}());

1

let person1 = new Person('小明');

这样person1就有它的私有name属性了，外部无法直接访问或修改改属性。等等，似乎有什么问题，如果我们再实例化一次Person呢？

1
2
3

let person1 = new Person('小明');
let person2 = new Person('大明');
console.log(person1.getName()); // 大明

改进

为了让每个实例拥有自己的私有属性，相互之间不影响，我们可以引入一个id作为每个实例的唯一标识，这样就实现了真正的私有属性：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

const Person = (function() {
  const private = {};
  let privateId = 0;

  function Person(name) {
    this._privateId = privateId++;
    private[this._privateId] = {};
    private[this._privateId].name = name;
  }

  Person.prototype.getName = function() {
      return private[this._privateId].name;
  };

  return Person;
}());

let person1 = new Person('小明');
let person2 = new Person('大明');
console.log(person1.getName()); // 小明

1
2

person1._privateId = 111;
console.log(person1.getName()); // 报错

所以我们改为用Object.defineProperty方法申明_private属性，防止它被更改。

1
2
3
4
5
6
7

Object.defineProperty(this, '_privateId', {
  value: privateId++,
  writable: false, // 设为不可写，_privateId就不会被更改了（其实默认就是false）
});
this._privateId = privateId++;
private[this._privateId] = {};
private[this._privateId].name = name;

至此，我们仅用es5的特性就实现了私有属性，而然该方法还有以下几个弊端：

• 即便Person的某个实例对象被垃圾回收了，private对象里存储的它的全部私有属性依旧不会被回收，这会导致内存泄漏问题
• 每个实例对象多出了一个_privateId属性，而且该方法不够直观优雅

WeakMap了解一下？

既然我们不想多造一个单独的_privateId属性去实现私有属性的存储，那还有什么值可以作为该实例对象的唯一标识呢？它的内存地址？可是js似乎不允许直接获取一个对象的地址。直接拿对象本身作为key可以吗？

1
2

private[this] = {};
private[this].name = name;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

const Person = (function() {
  const private = new WeakMap();

  function Person(name) {
    private.set(this, {});
    private.get(this).name = name;
  }

  Person.prototype.getName = function() {
      return private.get(this).name;
  };

  return Person;
}());

let person1 = new Person('小明');
let person2 = new Person('大明');
console.log(person1.getName()); // 小明

现在代码看上去简单优雅了很多，我们不再需要额外的id去标识每个实例，那内存泄漏问题呢？这就是为何要用WeakMap而不是Map了，WeakMap对key对象仅有“弱引用”，当没有其它引用指向该key对象时，该对象即可被垃圾回收，WeakMap不会阻止回收。

其实用WeakMap实现私有属性本身是比较简单的，但了解其背后的原因和原理更加重要。