2018-10-17

Javascript的尾递归及其优化

在平时的代码里，递归是很常见的，然而它可能会带来的调用栈溢出问题有时也令人头疼：

我们知道， js 引擎（包括大部分语言）对于函数调用栈的大小是有限制的，如下图（虽然都是很老的浏览器，但还是有参考价值）：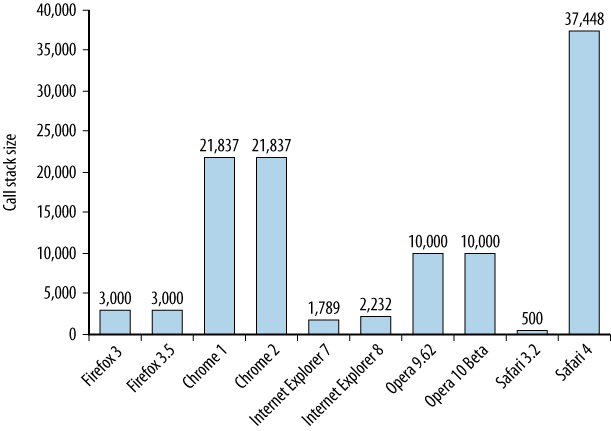

为了解决递归时调用栈溢出的问题，除了把递归函数改为迭代的形式外，改为尾递归的形式也可以解决（虽然目前大部分浏览器没有对尾递归（尾调用）做优化，依然会导致栈溢出，但了解尾递归的优化方式还是有价值的。而且我们可以通过一个统一的工具函数把尾递归转化为不会溢出的形式，这些下文会一一展开）。
在讨论尾递归之前，我们先了解一下尾调用，以及 js 引擎如何对其进行优化。

尾调用

当函数a的最后一个动作是调用函数b时，那么对函数b的调用形式就是尾调用。比如下面的代码里对fn1的调用就是尾调用：

const fn1 = (a) => {
  let b = a + 1;
  return b;
}

const fn2 = (x) => {
  let y = x + 1;
  return fn1(y);        // line A
}

const result = fn2(1);  // line B

我们知道，在代码执行时，会产生一个调用栈，调用某个函数时会将其压入栈，当它 return 后就会出栈，下图是对于这段代码简易示例的调用栈（没有对尾调用做优化）：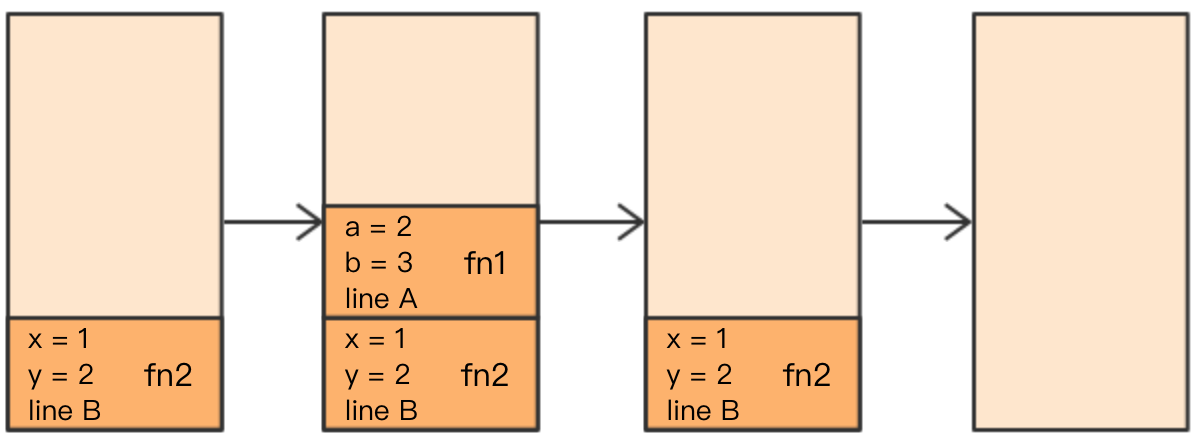

首先fn2被压入栈，x、y依次被创建并赋值，栈内也会记录相应的信息，同时也记录了该函数被调用的地方，这样在函数 return 后就能知道结果应该返回到哪里。然后fn1入栈，当它运行结束后就可以出栈，之后fn2也得到了想要的结果，返回结果后也出栈，此段代码运行结束。
仔细看一下以上过程，你有没有觉得第二第三步中fn2的存在有些多余？它内部的一切计算都已经完成了，此时它在栈内的唯一作用就是记录最后结果应该返回到哪一行。因而可以有如下的优化：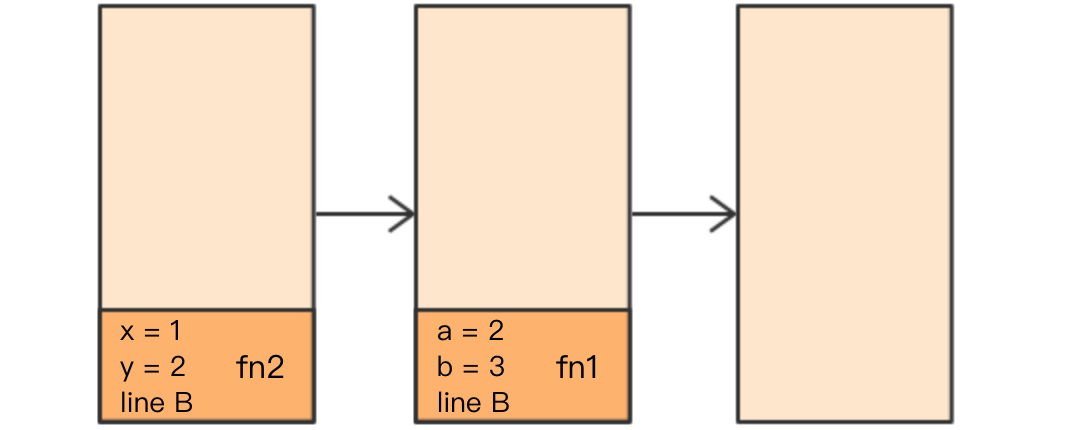

在第二步调用fn1时，fn2即可出栈，并把line B信息给fn1，然后将fn1入栈，最后把fn1的结果返回到line B即可，这样就减小了调用栈的大小。

辨别是否是尾调用

1
2
3

const a = () => {
  b();
}

这里b的调用不是尾调用，因为函数a在调用b后还隐式地执行了一段return undefined，如下面这段代码：

const a = () => {
  b();
  return undefined;
}

如果我们把它当做尾调用并按照上面的方法优化的话，就得不到函数a正确的返回结果了。

1 2	const a = () => b() \|\| c(); const a1 = () => b() && c();

这里a和a1中的b都不是尾调用，因为在它调用之后还有判断的动作以及可能的对于c的调用，而c都是尾调用。

const a = () => {
  let result = b();
  return result;
}

对于这段代码，有文章指出b并不是尾调用，即便它与const a = () => b()是等价的，而后者显然是尾调用。这就涉及到定义的问题了，我觉得不必过于纠结，尾调用的真正目的是为了进行优化，防止栈溢出，我测试了下支持尾调用的 safari 浏览器，在严格模式下用类似的代码执行一段递归函数，结果是不会导致栈溢出，所以 safari 对这种形式的代码做了优化。

尾递归

现在就轮到本篇文章的主角——尾递归了，看一下下面这段简单的递归代码：

const sum = (n) => {
  if (n <= 1) return n;
  return n + sum(n-1)
}

就是计算从1到n的整数的和，显然这段代码并不是尾递归，因为sum(n-1)调用后还需要一步计算的过程，所以当n较大时就会导致栈溢出。我们可以把这段代码改为尾递归的形式：

const sum = (n, prevSum = 0) => {
  if (n <= 1) return n + prevSum;
  return sum(n-1, n + prevSum)
}

这样就是尾递归了，这段代码在 safari 里以严格模式运行时，不会出现栈溢出错误，因为它对尾调用做了优化。那有多少浏览器会做优化呢？其实在 es6 的规范里，就已经定义了对尾调用的优化，不过目前浏览器对其支持情况很不好:
100%

具体见这里
即便将来大部分浏览器都支持尾调用优化了，按照 es6 的规范，也只会在严格模式下触发，这明显会很不方便。那我们把递归函数转为尾递归有什么用呢？其实我们可以通过一个统一的方法对尾递归函数进行处理，让其不再导致栈溢出。

Trampoline

Trampoline是对尾递归函数进行处理的一种技巧。我们需要先把上面的sum函数改造一下，再由trampoline函数处理即可：

const sum0 = (n, prevSum = 0) => {
  if (n <= 1) return n + prevSum;
  return () => sum0(n-1, n + prevSum)
}
const trampoline = f => (...args) => {
  let result = f(...args);
  while (typeof result === 'function') {
    result = result();
  }
  return result;
}
const sum = trampoline(sum0);

console.log(sum(1000000)); // 不会栈溢出

可以看到，这里实际上就是把原本的递归改为了迭代，这样就不会有栈溢出的问题啦。

当然，如果一个方法可以写成尾递归的形式，那它肯定也能被写成迭代的形式，但有些场景下使用递归可能会更加直观，如果它能被转为尾递归，你就可以直接用trampoline函数进行处理，或者把它改写成迭代的方法（或者等大部分浏览器支持尾递归优化后在严格模式下执行）

参考：
https://blog.logrocket.com/using-trampolines-to-manage-large-recursive-loops-in-javascript-d8c9db095ae3
http://2ality.com/2015/06/tail-call-optimization.html
https://www.zhihu.com/question/30078697/answer/146047599